Atanaska Dobreva, PhD

Assistant Professor, Department of Cellular Biology and Anatomy
Assistant Professor, Department of Mathematics
1201 Goss Ln, Augusta, GA 30912
Office: GE 2022
Email: adobreva@augusta.edu
Research
My research uses an interdisciplinary approach connecting experimental data with a variety of mathematical and statistical tools, such as modeling, sensitivity and uncertainty analysis, parameter estimation and optimal control in order to generate deeper understanding of immune and physiological processes and interactions and to help answer questions of clinical relevance regarding disease management and treatment. Currently, my main areas of investigation include: i) processes of cells in the eye, and ii) autoimmunity.
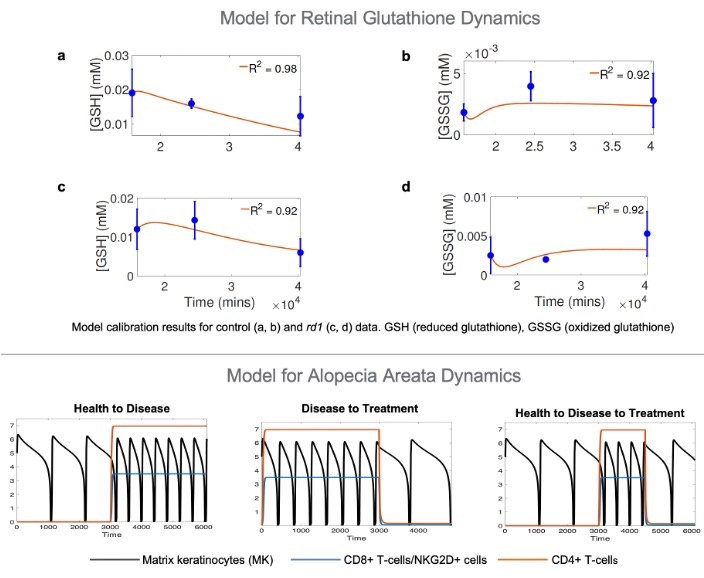
- In the realm of eye research, I focus on studying metabolic and antioxidant dynamics in the retina, the layer in the eye housing the light-sensitive cells responsible for vision, called photoreceptors. My work involves developing mathematical models for retinal metabolism in order to examine how interactions among key processes for resource supply, metabolic operations and energy production affect the vitality of retinal cells. This provides insight into the role of metabolites under shortage of nutrient or energy resources, which may elucidate mechanisms resulting in retinal diseases that lead to vision loss. Oxidative stress also plays an important role in the development of retinal diseases, as toxic reactive oxygen species, created due to exposure to light, high oxygen level in the eye blood vessels, and the high metabolic activity in the retina, interfere with the processes of retinal cells. Through mathematical modeling, I study the dynamics and interactions of reactive oxygen species and the glutathione antioxidant system in the retina. For model calibration and validation, we use experimental data from mice (see top figure panels). Findings from model analysis help to identify mechanisms with the highest potential impact, which could be translated into interventions for retinas severely affected by oxidative stress.
- In the area of autoimmunity, I investigate the autoimmune hair loss disease alopecia areata, which has no cure, and current therapies fail in many patients. Alopecia areata presents with distinct spatial patterns (round or oval hairless patches) and occurs as the immune system attacks hair follicles, disrupting their cycle through phases of growth, regression and rest, and severely reducing the duration of hair growth. My work develops mathematical models for processes involved in hair growth and their interactions with the main immune mediators driving the disease. Model simulations demonstrate disruption and shortening of the hair growth phase in response to the immune attack aimed at hair follicles (see lower figure panels). My study of alopecia areata also involves tackling questions about the design of observational studies that can inform the autoimmune hair loss models, so they can be used for in-silico examination of patient-specific disease presentation and response to therapies.
Education
Ph.D. Mathematics, Florida State University, 2018
M.S. Mathematics, Florida State University, 2014
B.A. Mathematics and Economics, Marymount University, 2010
Postdoctoral Training
Postdoctoral Research Scholar, Arizona State University, July 2020 - June 2022
Research Training Group Postdoctoral Scholar, North Carolina State University, July 2018 - June 2020